打造CP值最高的跨廠牌發射機 Deviation - DEVO10【固定下載】

johniu

原帖由 suvsuvsuv 於 2013年2月24日 10:11 PM 發表
目前已知2.3.5之后对a7105芯片（flysky, hubsan4)的高频进行初始化/对频操作时就会重启，2.3.3之前没有这个bug，如果使用a7105高频头请暂时刷回2.3.3版本。
2.3.5版本主要是同步了PB在春节期间的大量改动，我还需要花些时间 ...

抄收 suv大辛苦了 由衷滴感谢您

coldfire

今天clone了suv兄的D10源码。大致找到了bug的位置而且写了一个临时的解决方案。

Flysky重启的问题在两个（貌似）不相关的时间出现：

rev 1091：出现问题的文件是src/target/common_devo/syscalls.c

改动只有一行：
旧代码：fd = (strcmp(file + strlen(file) - 4, ".fon") == 0) ? 4 : 3;
新代码：fd = (strcmp(file + strlen(file) - 4, ".fon") == 0) || strncmp(file, "protocol/", 9)== 0 ? 4 : 3;
我实在想不出来是什么原因，但是新的代码会让D10重启

rev 1097：这一版里，即使用旧的syscalls.c系统还是会重启。这次更新的规模很大，包括Flysky_a7105.c，但据我观察似乎不是重启的原因。最后我发现似乎src/target/common_devo/clock.c是造成重启的原因，用上一版的文件替代就可避免重启。

所以我的最终方案是用suv兄最新的版本的代码，把syscalls.c用rev1090替换，把clock.c用rev1096替代，编译结束就得到可用的dfu文件。我飞了v911 (flysky), minicp (devo)，目前没有发现明显问题。

因为我对系统非常生疏（惭愧，今天才拜读代码），改变代码造成何种潜在问题还不清楚，还是盼望suv兄能早日给出更完美的方案！

hmjack2008

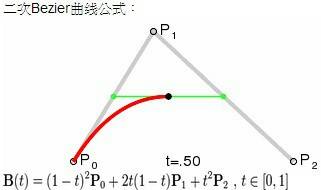
關於 擬合曲線 :
(1) 之前我採用 "不通過 控制點(Spline By Points)" 的 Bezier(貝茲)二次曲線 :
http://www.rctw.net/forum.php?mod=viewthread&tid=241130&page=72#pid2021403
可以快速的計算, 但因為不通過控制點, 因此控制點與實際曲線有偏離.


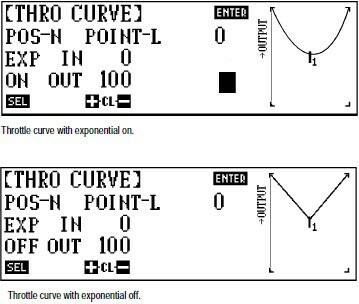
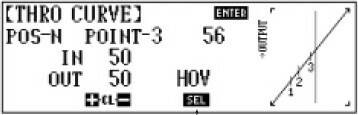
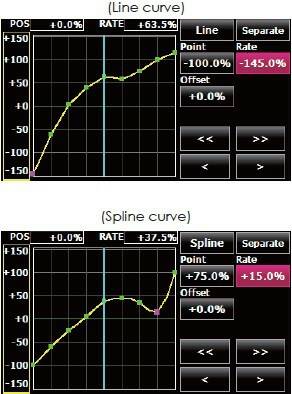
(2) 查閱了JR pcm10 與 Futaba 18mz的手冊:
兩個控都可以在 "任意X位置" 新增點來生成通過控制點的曲線.
實際操作JR10S時發現其實相鄰兩個X位置無法小於(12%, JR10S是 min~max : 0~100%)





(3) 之後查閱了,Bezier(貝茲)曲線原理,又發現了其他通過控制點(Spline by Points)的作法:
http://zh.wikipedia.org/wiki/貝茲曲線
http://blog.csdn.net/microchenhong/article/details/6316332


(4) 我用Excel試作了AGG(Anti-Grain Geometry) Bezier Curves,
可以用 k(%) 調整曲線扭曲程度.
才發現兩個相鄰兩個X位置(-10 與 0)太接近會造成曲線過度扭曲(這個相鄰值與JR10S相當).

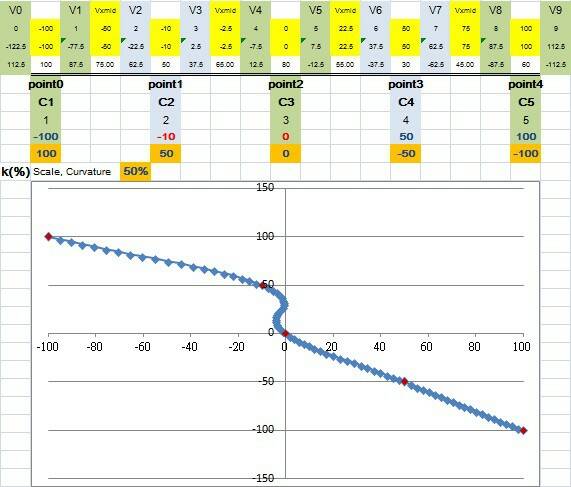
(5) 最後, 將此 AGG Bezier Curves 用 DEVO10模擬器 實現如下:
計算主要和上次的不通過控制點方式一樣,只是先擴增虛擬控制點.
X位置仍然採用(範圍:-10000~+10000) n個點等區分.
curves_Bspline2.zip (3.1 KB, 下載次數: 160)

2013年2月25日 12:28 PM 上傳

點擊文件名下載附件

通過 控制點(Through Points):


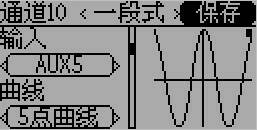
之前的 不通過 控制點(Spline By Points):


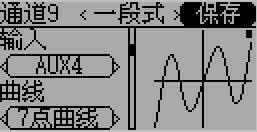
(6) 若要做到如同JR或Futaba可以在 "任意X位置" 新增點,將需要解一元二次方程.
關鍵點在 如何"快速開根號" !!

[ 本帖最後由 hmjack2008 於 2013年2月25日 02:00 PM 編輯 ]

coldfire

整点数求根应该不难，性能应该也不差，就是迭代，基本运算是加减法和移位。

下面转自wiki：

short isqrt(short num) {
    short res = 0;
    short bit = 1 << 14; // The second-to-top bit is set: 1L<<30 for long

    // "bit" starts at the highest power of four <= the argument.
    while (bit > num)
        bit >>= 2;

    while (bit != 0) {
        if (num >= res + bit) {
            num -= res + bit;
            res = (res >> 1) + bit;
        }
        else
            res >>= 1;
        bit >>= 2;
    }
    return res;
}

suvsuvsuv

原帖由 coldfire 於 2013年2月25日 11:51 AM 發表
今天clone了suv兄的D10源码。大致找到了bug的位置而且写了一个临时的解决方案。

Flysky重启的问题在两个（貌似）不相关的时间出现：

rev 1091：出现问题的文件是src/target/common_devo/syscalls.c

改动只有一行：
旧代码：fd ...

我目前定位的原因是在clock.c, PB为了实现崩溃前记录错误日志，非常频繁的清除某个外部中断，修改的代码看上去没有任何问题，但是经过验证是起到了反效果--原来很稳定的系统变成很容易重启。我昨天已经将clock.c回滚到之前的版本并小范围发送给有重启问题的模友验证，您可以到这个地方下载并告知问题是否消失 ：http://61.238.246.202/deviation/devil10/devo10-v2.3.8.zip

hmjack2008

原帖由 coldfire 於 2013年2月25日 12:07 PM 發表
整点数求根应该不难，性能应该也不差，就是迭代，基本运算是加减法和移位。
下面转自wiki： ...

若沒有其他更快的 , 我也打用此方法 !!

(之前在看  牛顿迭代法 與 卡马克算法 (John Carmack))