打造CP值最高的跨廠牌發射機 Deviation - DEVO10【固定下載】

ANDYr1211

改天好好看這一篇
謝謝分享

hmjack2008

原帖由 suvsuvsuv 於 2013年2月5日 11:00 AM 發表
按鍵(Up;Dn)與(R;L)互換会改变所有界面的操作习惯（目前都是Up/Dn切换按钮、选项），无法实现，但是可以将Listbox界面改到右侧显示，附件最新版本已经按照您的建议调整了界面 ...

感謝 !!
可否提供模擬器... 因為bitbucket.org/sunvsuv/devil10網站一直沒更新,我無法下載自行編譯 !!

hmjack2008

原帖由 suvsuvsuv 於 2013年2月5日 11:00 AM 發表
2）拟合曲线目前找不到合适的计算公式，所以暂时无法实 ...

我所採用的"二次B 样条曲线", 不通過 "點", 會有偏離, 但計算較簡易 !!



excel的試算:



模擬器(會有偏離):




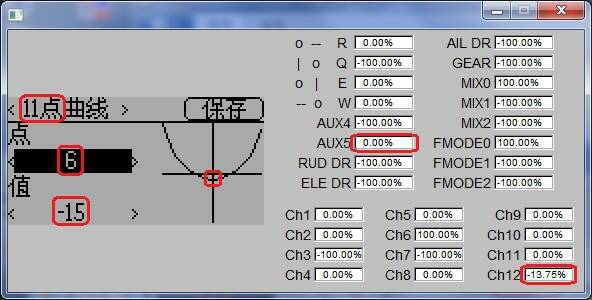
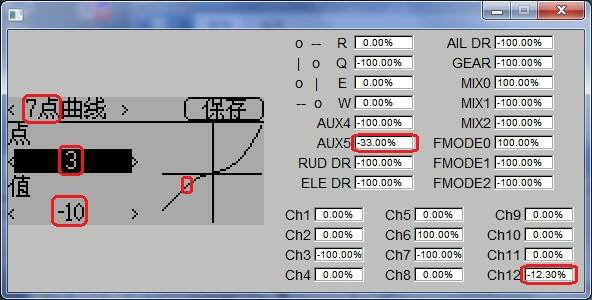
網絡上原本提供的是: f(t)函式
即 X=f1(t), Y=f2(t),
但遙控器需要的是 Y=f(x),
因此需要先用 X解二次方程( 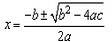)得到t, 再用t計算Y.
但X若是線性, 即n-點的位置(X值)是固定的 =(CHAN_MAX_VALUE-CHAN_MIN_VALUE)/n.
則t可用內插法直接得出較為快速.

1. /********** Bspline **********/
   
2. s16 Bspline(struct Curve *curve, s32 value) // use n-POINT
   
3. {
   
4.     s32 x0,x1;
   
5.     s32 y0,y1,y2;
   
6.     s32 b0,b1,b2;
   
7.     s32 t,tmp;
   
8.     int i;
   
9.     int num_points = (curve->type - CURVE_3POINT) * 2 + 3;
   
10.     s32 step = 10000/(num_points-1) ; // (2*10000)/(2*(num_points-1) ,use 2n-steps for n-POINT
    
11.     for (i = 0; i < num_points; i++) {
    
12. 
    
13.         x0 = -10000 + (2*i-1)*step; // n-POINT, X is linear
    
14.         x1 = x0 + 2*step;
    
15.                
    
16.         if(value >= x0 && value <= x1) {
    
17.                         y1 = curve->points;  
    
18.                         if (i==0) { // end point
    
19.                                         y2 = curve->points[i+1];
    
20.                                         y0 = y1+y1-y2; // Linear extension
    
21.                         } else {
    
22.                                 if (i==(num_points-1))        { // end point
    
23.                                         y0 = curve->points[i-1];
    
24.                                         y2 = y1+y1-y0; // Linear extension
    
25.                                 }
    
26.                                 else {
    
27.                                         y0 = curve->points[i-1];
    
28.                                         y2 = curve->points[i+1];
    
29.                                 }
    
30.                         }
    
31.                         
    
32.                         b0=100*(y1+y0)/2;  // mid
    
33.                         b1=100*(y1-y0);  // delta1
    
34.                         b2=100*(y2-2*y1+y0)/2; // (delta2-delta1)/2
    
35.                         /*** t = (value-x0)/(x1-x0), use interpolate because X is linear ***/
    
36.                         t = 50*(value-x0)/step; // 2-decimals: (100*(value-x0))/(2*step)
    
37.                         tmp = b0+b1*t/100+b2*t*t/10000; //Bspline
    
38.                         // tmp = b1*t/100+y0;  //Interpolate
    
39.             return tmp;
    
40.         } //if(value >= x0 && value <= x1)
    
41.     } //for (i = 0; i < num_points; i++)
    
42.     return PCT_TO_RANGE(curve->points[num_points-1]);
    
43. }
    
44. /********** Bspline **********/
    

複製代碼

模擬器: (7點 與 11點 用 Bspline擬合曲線, 僅作為此範例之用)
emu_devo10_Bspline.zip (310.46 KB, 下載次數: 123)

2013年2月6日 12:53 PM 上傳

點擊文件名下載附件

[ 本帖最後由 hmjack2008 於 2013年2月6日 12:53 PM 編輯 ]

hmjack2008

原帖由 davidlitmanen 於 2013年2月5日 04:13 PM 發表
是的了解。小弟提一個不學無術的方法，內建81點(比如)，但只開放原來的點數設定；配合雲線法只做一次之後列表，用查表法做兩點內插。至於列表的時機點，應該就是那個Auto按下去的瞬間吧?! ...

或者 : 在設定時將 參數計算出(解方程)並儲存參數,後續混控時利用已儲存的 參數 即時計算.




[ 本帖最後由 hmjack2008 於 2013年2月6日 01:09 PM 編輯 ]

suvsuvsuv

原帖由 hmjack2008 於 2013年2月6日 01:08 PM 發表

或者 : 在設定時將 參數計算出(解方程)並儲存參數,後續混控時利用已儲存的 參數 即時計算.
851903

851904

这种 方式是非常有效可行的，如果是设计商业遥控我也会这么做，但是deviation使用了文本文件来传递模型文件，导致难以存储大量的曲线拟合值。

suvsuvsuv

原帖由 hmjack2008 於 2013年2月6日 11:23 AM 發表

感謝 !!
可否提供模擬器... 因為bitbucket.org/sunvsuv/devil10網站一直沒更新,我無法下載自行編譯 !!

从PB引入devo7e的修改后，我的repository就改回到下述url了
https://bitbucket.org/sunvsuv/deviationfor6810